ドル・コスト平均法の活用について【ETF投資戦略㊽】

積み立て投資の中で、一定のインターバルで定額で同じ商品を買い付ける方法をドル・コスト平均法という。一定のインターバルは毎日、毎月や四半期等と様々で、勤労層にとっては、毎月給与が入るので、毎月積み立てることは、取り組みやすい方法である。新NISAのつみたて投資枠を利用する際には、この方法を使うことが多いと思われる。今回は、このドル・コスト平均法の特性について簡単な分析を行ってみたい。

ドル・コスト平均法のポイントは、（毎月など）定めたインターバル毎に一定額の投資を行うことで、簿価の変動を安定化させ、投資した銘柄や投資信託の値上がりを待つことである。株式は長期的には上昇するとされているものの、短期的には下落することもある。それ故、ドル・コスト平均法は投資タイミングに自信がなくても、投資を行いやすい方法である。株価が単純に振動するパターンでのドル・コスト平均法の簿価との関係を図1、図2に示した。図1は株価が下落から始まるパターン（ケース1）、図2は株価が上昇から始まるパターンである。また、株価は100円からスタートし、90～110円の間を振動するとする。

図1　株価と簿価の推移（ケース1：当初、株価が下落）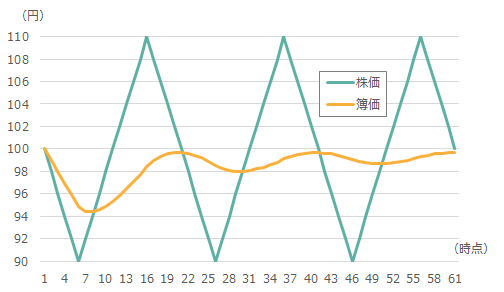

図2　株価と簿価の推移（ケース2：当初、株価が上昇）

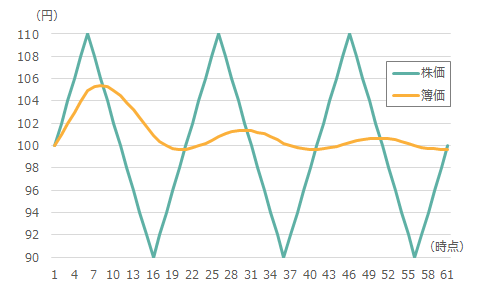
図1は株価が下げから始まるので、簿価も低下から始まっているもの、徐々に簿価が上昇し100円近くになっている。一方、図2は株価が上げから始まり、簿価はいったん高くなるが、徐々に低下して100円近くになっている。

次に図3に、ケース1、ケース2において毎回の買い付け額を1万円として投資した際の評価損益の推移を示した。

図3　評価損益の推移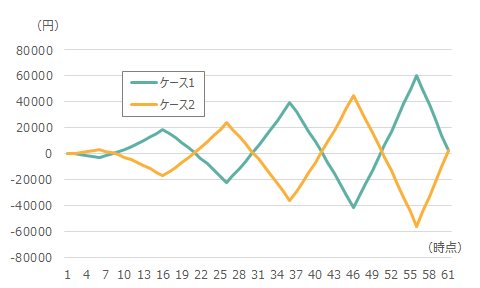

※評価損益は、（各時点における株価－投資開始からの平均簿価）×買付済み株数で計算。

株価は同じように動くとしても、下げから始まるか、上げから始まるかで評価損益が対称的に推移しており、図1、2でみたように時間が経過するにつれて、簿価が安定化していく代わりに、評価損益の振幅は大きくなる。このようにドル・コスト平均法は、定額投資を行うことで、簿価を安定化させて、長期の上昇を待つ戦略である。

そして、図1は株価が下げから始まることで簿価は100より下の期間が長いのに対して、図2は100より上の期間が長いので、評価損益が対称的に見えるものの、最大評価益（図のそれぞれの頂点）になるにはケース1の方が早い。逆に言えば、下げから始まったとしても、気を落とさず、気長に積み立てることが大切であるともいえよう。
　
次に、最初から下落した場合、どの程度が損益分岐点になるかを試算してみよう。簡単にするために3期間投資を考える。毎回の買い付け額は1万円とする。例えば、時点1の株価は100円、時点2の株価が10円に下落した時、時点3で評価損益がゼロになるにはどの程度の株価になる必要があるだろうか？

この場合、答えは18.2円程度である。これは、時点2での株価が下がるほど購入できる株数が増えて加重平均された簿価が下がり、時点3で評価損益がゼロに戻るための株価も下がっていくためである。つまり、株価が下がった時に多く買い付けできた結果、平均買い付けコストが下がり、株価が少し戻った時に評価損益が大きく上がったということである。

ということで、投資を始めて最初から下落したとしても、一定金額で買い付けていた場合、評価益になるには元の株価に戻る必要はないということが分かるだろう。図4にもう少し一般化したものを示した（原理的なものに興味のある方は末尾の（ご参考）を参照されたい）。

図4　時点1で100円で1万円を投資し時点2で追加で1万円を投資した場合に、
時点3で評価損益がゼロに戻る株価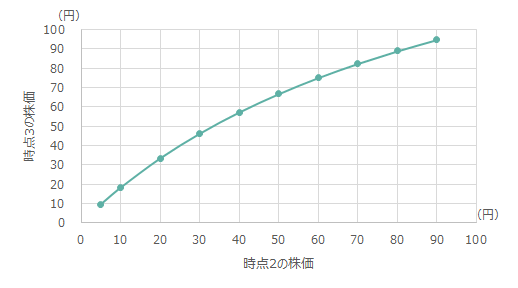

もっとも、100円で投資した株価がいきなり10円に下がるとかなりショックを受けて、投資を続けるかという別の問題が生じるかもしれない。

インデックス投資の例で言えば、1989年12月末の日経平均株価は38,915.87円だったが、その後、株価は下落を続け、リーマン・ショック後の2009年2月末には7,569.42円まで下落している。約80.55％の下落である。これを上記の3期間モデルに当てはめると、12,672.31円程度が損益分岐点となる。図4でいえば、横軸に示される時点2の20円近くに対応する時点3の株価となる。

勿論、個別銘柄はその企業が倒産すると損失確定となる。インデックスに連動する投資信託やETFでは償還となると損益確定となるが、分散されている分だけ、個別銘柄投資に比べて、その可能性は低いと考えられる。当初下落しても気長に積み立てることが大切であるといえよう。

（ご参考）
毎月末にある銘柄に１万円投資するとしよう。話を簡単にするために3回の投資を考える。そして、3回目に投資した時の投資した株数と簿価、評価益を考えてみたい。各時点の株価をP₁、P₂、P₃とすると、各時点で購入した株数は10000/P1、10000/P2、10000/P3となる。購入した株数合計は10000×（1/P1＋1/P2＋1/P3）となる。ここで括弧の中をH3と表すことにしよう。
時点3の簿価（B3）は、投資合計/株数合計となるから、（3×10000）/（10000×H3）＝3/H3となる。時点3での評価損益（E3）は（時点3の株価－時点3の簿価）×時点3の株数合計＝（P3－B3）×（10000× H3）となる。この評価損益E3は、
　E3＝（P3－B3）×10000× H3
　　＝（P3－3/H3）×10000×H3
　　＝（P3×H3－3）×10000
　　＝（P3×（1/P1＋1/P2＋1/P3）－3）×10000
　　＝（P3×（1/P1＋1/P2）－2）×10000　　　　①
と表すことができる。ここで、P3＝kP1、P2＝mP1とする。但し、k>0、m＞0とする。
　E3＝10000×（（1/k＋1/m）－2）　　　　②
E3>0となるためには、
k＞2m/（m＋1）　　　③
であればよい（図4は、k＝2m/（m＋1）として、描いたものである）。
例えば、m＝0.1　なら、k＞2×0.1/（0.1+1）＝0.1818181818、、。
つまり、株価が時点2で10分の1になっても、時点3で時点1比で約0.182倍より大きければ利益が出るということである。
　なお、上記の説明は、時点3でも購入した場合である。購入する直前の状態で見ると、

評価損益（E3'）＝（時点3の株価－時点2の簿価）×時点2の株数合計
　　　　　　　　＝（P3－B2）×10000×H2
　　　　　　　　＝（P3－2/H2）×10000×H2
　　　　　　　　＝（P3×H2－2）×10000
　　　　　　　　＝（P3×（1/P1＋1/P2）－2）×10000　　④
と、①式と同じになる。