負けないためのETF投資戦略
バランス型運用と為替【ETF投資戦略㉘】
この記事は、約5分で読めます
本コラム第6回「外債投資と為替」で、一般的には為替ヘッジなしの方が為替ヘッジありに比べて、リスク量は大きくなるが、ある条件下では逆転するケースがあることを示した。最近、バランス型投資信託でもそうした現象が見られるようになってきた。国内ETFでも為替ヘッジあり、なしの選択肢が増えてきているので、どのような条件下でそうした現象が生じるのか、簡単に分析を行ってみたい。
簡便化のため、米国株と米国債に投資することを考える。図1にそのリスクを示した。バランス型の運用ということで株式50%、債券50%とした。
図1 米国株50%・米国債券50%のバランス型運用の為替ヘッジあり、なしのリスク量の推移(期間:1992年1月末~2022年6月末、月次)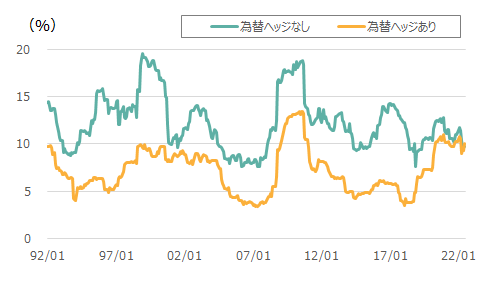
注)米国株はS&P500、米国債はブルームバーグUSアグリゲート指数。月次リバランス。月次リターンを用いて算出した標準偏差(年率換算)を24か月ローリングで表示。直近は6月末。
出所)Bloombergよりウエルス・スクエア作成。
多くの場合、為替ヘッジなしのリスク量が大きいが、直近では逆転していることがわかる。分析を行うにあたり、本コラム第6回の枠組みを再度利用するが、今回は株式も加わることで、より複雑になる。ポイントの一つは、株式と為替、債券と為替の相関の状況である。図2に株式と為替、債券と為替の相関係数の推移を示した。なお、定式化について、巻末のご参考に示した。ご興味のある方は参照されたい。
図2 株式、債券と為替(ドル円)の相関係数の推移(期間:1992年1月末~2022年6月末、月次)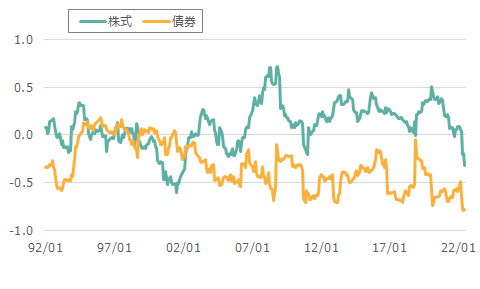
注)米国株はS&P500、米国債はブルームバーグUSアグリゲート指数。月次リターンを用いて算出した相関係数を24か月ローリングで表示。直近は6月末。
出所)Bloombergよりウエルス・スクエア作成。
債券と為替の逆相関は、2000年代に入り継続しているが、ここにきて、株式と為替の相関がマイナスとなってきたことが、為替ヘッジあり、なしのリスク量の逆転に影響を与えていると考えられる。
巻末のご参考で示した式をもとに、株と為替の相関、債券と為替の相関の関係から、どのような相関を示したときにこのリスク量の逆転が生じるかを図3に図示してみた。
図3 為替ヘッジありが為替ヘッジなしのリスク量を上回る際の株、債券と為替の相関関係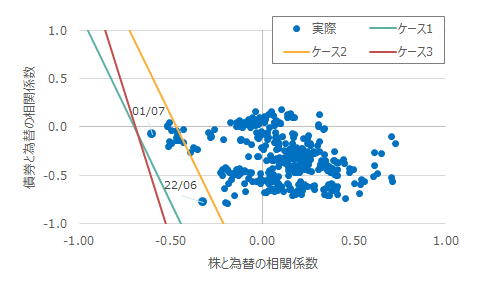
注)ケース1は1990年2月~2022年6月で計測したリスク量で計算、ケース2は2020年7月~2022年6月で計測したリスク量で計算、ケース3は1999年8月~2001年7月で計測したリスク量で計算したもの。各時点よりさかのぼる24か月間のデータより計算したものをプロットしたもの。
出所)Bloombergよりウエルス・スクエア作成。
図には、株と為替の相関係数、債券と為替の相関係数の組み合わせをプロットしたものと、3本の直線を示しており、相関係数は-1~+1の範囲である。直線より左下の部分の範囲で株と為替、債券と為替の相関係数のプロットがあれば、為替ヘッジありが為替ヘッジなしのリスク量を上回っていることになる。ケース1は全期間で計測した株、債券、為替のリスク量を用いた場合の直線、ケース2は2020年7月~2022年6月の24か月間のリスク量を用いた場合の直線、ケース3は図1で株と為替の相関が-0.6に達した2001年7月からさかのぼる24か月で計測した場合の直線である。
ケース2では、2022年6月の相関係数のプロットが、直線より左下に来ている。一方、ケース3の場合は、直線より左下のケースはない。実はこのときは、2001年7月に株と為替の相関が-0.6に達していたにも関わらず、債券のリスク量がケース2より小さかったため(株のリスクと債券のリスクがよりアンバランスになった)、直線自体が左にシフトしてしまい、為替ヘッジありの方が為替ヘッジなしに比べてリスク量が大きくはならなかった(図1でも確認できる)。また、株と債券のリスク量の比が変化すると、直線の傾きが変化する。長期的には安定した関係があるかもしれないが、短期的には変化する点には注意が必要である。
こうした現象が、長い期間にわたると、商品設計、実際の運用手法、評価の枠組みに影響を与える。足元の世界的インフレが長期化することで、海外金利上昇(債券価格下落)・円安・海外株安の関係、すなわち債券と為替、株と為替の逆相関状態が続くことで、為替ヘッジあり、なしのリスク量の逆転が継続することもあり得る。ETFを利用するにあたっても、為替ヘッジあり、なしを使い分ける際には、留意しておきたい。
(ご参考)
株と債券の2資産のバランス型運用を考えてみよう。株も債券も日本から同じ国(例えば米国)に投資するとする。為替ヘッジをしないポートフォリオのリターンをRp1、為替ヘッジをするポートフォリオのリターンをRp2とする。
また、現地株式のリターンをRs、現地債券のリターンをRb、為替のリターンをRe、為替ヘッジコストをRhとする。同様にリスクをそれぞれσs、σb、σeとする。また相関係数をρで示し、株式比率をx、債券比率を1-xとする。
為替ヘッジをしないポートフォリオのリターンRp1は、
Rp1=(xRs+(1-x)Rb )+Re
と表すことができる。
一方、為替ヘッジを行った場合のリターンRp2は、
Rp2=(xRs+(1-x)Rb )+Rh
と表すことができる。為替ヘッジコストRh≒内外短期金利差とする。
次に、為替ヘッジなしのポートフォリオの分散は、
σp12=x2σs2+(1-x)2σb2+σe2+2x(1-x)ρs,bσsσb+2xρs,eσsσe
+2(1-x)ρb,eσbσe ①
と表すことができる。
また、為替ヘッジありのポートフォリオの分散は、σh2=0と仮定して、
σp22=x2σs2+(1-x)2σb2+2x(1-x)ρs,bσsσb ②
となる。
為替ヘッジありのリスク量が、為替ヘッジなしのリスク量より大きくなるということは、
σp22-σp12>0 ③
である。
そこで、③式に、①、②式を代入すると、
σp22-σp12
=(x2σs2+(1-x)2σb2+2x(1-x)ρs,bσsσb)-(x2σs2+(1-x)2σb2+σe2+2x(1-x)ρs,bσsσb+2xρs,eσsσe+2(1-x)ρb,eσbσe)
=-(σe2+2xρs,eσsσe+2(1-x)ρb,eσbσe)>0 ④
となる。
両辺をσeで割ると、
σe+(2xρs,eσs+2(1-x)ρb,eσb))<0
σeを右辺に移した上で、両辺を2で割ると、
(xσs)ρs,e+((1-x)σb)ρb,e<-1/2σe ⑤
となる。
A=xσs 、B=(1-x)σb、C=-1/2σe、X=ρs,e、Y=ρb,eとすると、AX+BY<Cの不等式となる。A、Bの相対的な大きさで直線の傾きが変化する。また、X、Yは相関係数なので、いずれも-1~+1までの間をとる。
一例として、株式と債券を50%ずつ保有したバランス型の運用の場合、⑤式は
(1/2σs)ρs,e+(1/2σb)ρb,e<-1/2σe
両辺を1/2で割ると、
σsρs,e+σbρb,e<-σe
となる。
仮にσs=15、σb=6、σe=9とすると、
15ρs,e+6ρb,e<-9
となり、両辺を3で割ると
5ρs,e+2ρb,e<-3 ⑥
となる。
この⑥式の具体的なイメージを下の図に示した。この直線より左下で株と為替、債券と為替の相関係数の組み合わせがあれば、為替ヘッジなしのリスク量が為替ヘッジありのリスク量より小さくなるゾーンである(相関係数は-1~+1の範囲)。
直線は、株50%のケースに加えて、株30%、70%のケースを示した。各資産のリスク量は上記の例と同じとしている。株式比率が高くなると、直線はより垂直に近くなり、債券と為替と相関係数の大小と関係はなくなり、株と為替の相関で規定されていく。一方、債券比率が多いと直線は水平に近くなり、債券と為替の相関係数の状態で規定されていく。
図 為替ヘッジありが為替ヘッジなしのリスク量を上回る相関係数の状態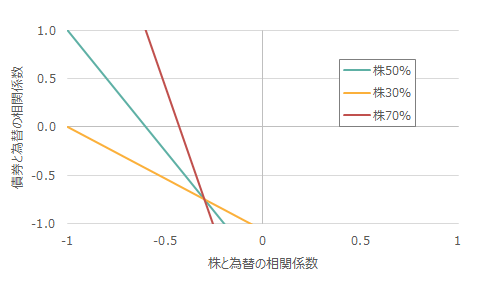
<指数の著作権等について>
S&P 500 指数はスタンダード&プアーズ ファイナンシャル サービシーズ エル エル シーの所有する登録商標であり、野村アセットマネジメントに対して利用許諾が与えられています。スタンダード&プアーズは本商品を推奨・支持・販売・促進等するものではなく、また本商品に対する投資適格性等に関しいかなる意思表明等を行なうものではありません。
「Bloomberg®」は、Bloomberg Finance L.P.および、同インデックスの管理者であるBloomberg Index Services Limitedをはじめとする関連会社(以下、総称して「ブルームバーグ」)の商標およびサービスマークです。ブルームバーグまたはブルームバーグのライセンサーは、ブルームバーグ・インデックスに対する一切の独占的権利を有しています。
(2022年7月作成)


