負けないためのETF投資戦略
新興国株ETFの市場価格と基準価額の乖離について【ETF投資戦略55】
2024年10月25日作成
本コラム第52回で複数の国内上場ETFにおける市場価格と基準価額の乖離率を分析した。その中で、新興国株の乖離率の標準偏差が最も大きかった。今回は、この背景について簡単に分析を行いたい。
まず、図1に10本の国内上場ETFの乖離率を示した。ここでいう乖離率は、(市場価格/基準価額-1)×100で算出したものする。野村アセットマネジメントが運用するものを利用する。
図1 乖離率の平均と標準偏差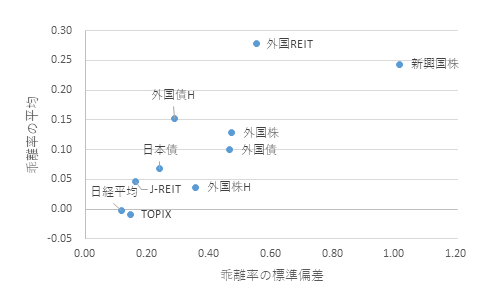
注)計測期間は2023年1月4日~2024年10月8日。分析対象は、日本債はNF・国内債ETF、TOPIXはNF・TOPIX ETF、日経平均はNF・日経225ETF、J-REITはNF・J-REIT ETF、外国株はNF・外国株ヘッジ無ETF、外国株HはNF・外国株ヘッジ有ETF、外国債はNF・外国債ヘッジ無ETF、外国債HはNF・外国債ヘッジ有ETF、新興国株はNF・新興国株ヘッジ無ETF、外国REITはNF・外国REITヘッジ無ETF(いずれも愛称で表示)。乖離率の平均や標準偏差は日次データより。
原資産が国内資産を対象としたETFの乖離率の標準偏差は小さく、外国資産を対象としたETFはその標準偏差が大きい。特に新興国株は大きい。
乖離率は、第52回で解説したように、国内資産を対象としたETFの場合、基本的には市場での需給と考えられる。一方、海外を対象とした国内上場ETFの場合には、基準価額の算出が前日の終値に当日のTTM為替レートをかけて算出する。従って、当日の終値までの時間差分だけ、原資産や為替の変動の影響が加わる。つまり、
国内対象ETFの乖離率=需給 ①
海外対象ETFの乖離率=原資産等リターン+為替のリターン+需給 ②
と、まとめることができよう。①の国内対象でも、日経平均やTOPIX等のように先物が存在していれば、乖離率は小さくなると考えられる。ところが、海外資産が対象の場合、今回取りあげる複数の国に分かれていることで、複数の原資産、対応する為替の動きを反映したものと考えられるが、時差や休日の違いもあって、複雑である。また、このETFは金銭拠出型であるため、設定や解約の費用も価格に反映される可能性がある。
では、本題の新興国株ETFの乖離率を回帰分析を用いて行ってみよう。ここでいう新興国株は、MSCI新興国株価指数を原指数としており、中国、インド、台湾、韓国のウエイトが上位で75.3%を占めている(2024年9月末時点)。また、これらの国の取引時間は、東証の取引時間と大小の違いはあれ、重複している。そこで、中国、インド、台湾、韓国の株価指数とドル円の動きで説明することを試みることにしたい。
分析にあたって、被説明変数を市場価格と基準価額の乖離率とする。説明変数を4~5個用意する。一つ目として、為替を考える。ドル円を用い、当日のTTMレートから東京終値の変化率とする(ETF市場は15:00で終わるので、ドル円東京終値とは時間がずれる点には注意)。次に株価の方は、新興国株指数に占める中国株の特性を鑑み、ハンセン中国企業株価指数、インドはSENSEX株価指数、台湾は加権指数、韓国は韓国総合株価指数を使用する。それら株価指数は、前日からの変化率で分析する。日本時間15:00では香港やインド市場は取引途中となるが、その時点でのリターンの方向と、それぞれの終値が同じ方向と仮定しているとみなす(インドとの重複時間がもっとも短い)。また、海外休日の場合、値は変化していないのでその間はリターンをゼロとし、市場が開いた日は、休日前からの変化率を計算し、分析を行った。
結果を表1に示した。
表1 新興国株ETFの乖離率の説明
| 為替 | ハンセン中企 | 台湾 | 韓国 | インド | 切片 | 決定係数 | |
| 回帰係数 | 0.50 | 0.20 | 0.15 | 0.20 | 0.08 | 0.23 | 0.397 |
| t値 | 4.13 | 8.57 | 3.38 | 4.13 | 1.54 | 5.86 | |
| 回帰係数 | 0.51 | 0.20 | 0.16 | 0.21 | 0.23 | 0.395 | |
| t値 | 4.21 | 8.59 | 3.54 | 4.49 | 6.00 |
注)分析期間は2023年1月4日~2024年10月8日まで。日次。為替は東京市場の終値-TTMレートの変化率、ハンセン中企はハンセン中国企業株価指数、インドはSENSEX株価指数、台湾は加権指数、韓国は韓国総合株価指数で日次の変化率。回帰分析として、上段では、ETFの乖離率=α+β1(為替)+β2(ハンセン中企)+β3(台湾)+β4(韓国)+β5(インド)として分析。下段はインドを除いて、韓国まで分析。表の2つの分析で、それぞれの上段は回帰係数で先の式のβ部分、切片はα部分を指す。下段はt値で回帰係数が統計的に意味があるか否かを示す。一般的に絶対値で2以上であれば有意とみなす。決定係数は自由度調整済。
出所)NRI SuperFocus、NRI Fundmark、Bloombergよりウエルス・スクエア作成。
これによると、全体の説明力は4割弱であった。説明変数の為替、ハンセン中国企業株、台湾株、韓国株の回帰係数はいずれも正の値であり、統計的には有意(t値が2以上)であった。インド株は重複時間が短いせいか、有意には少し届かなかった。それもあり、インドを除いても説明力(決定係数)の低下はわずかであった。
回帰係数はいずれも正の値で、ドル高円安になる、ハンセン中国企業株、台湾株、韓国株が前日より高くなると、乖離率は大きくなることを示す。韓国や台湾は日本と時差がなく、台湾の場合、日本時間で日本より早く終わり、韓国は30分遅い。香港は時差が1時間あり、現地時間で16時に終わる。多少の非重複時間を含むとしても、感覚的には理解できるだろう。
次に、ETFは市場取引であるものの、原資産の海外市場の休日等で設定・交換の申し込み不可日がある。このETFが金銭拠出型で、設定・解約時に費用がかかることから、申し込み不可日周辺の乖離率に影響が生じる可能性を考慮して、不可日の前日も含めて、ダミー変数(不可日とその前日を1、それ以外をゼロ)として扱うこととした。また、乖離率のラグ効果も考慮することにした。分析した結果が表2である。表1で有意でなかったインドを外した。
表2 新興国株ETFの乖離率の説明②
| 為替 | ハンセン中企 | 台湾 | 韓国 | 不可日 | 乖(t-1) | 乖(t-2) | 切片 | 決定係数 | |
| 回帰係数 | 0.40 | 0.21 | 0.13 | 0.21 | 0.24 | 0.29 | 0.15 | 0.06 | 0.557 |
| t値 | 3.80 | 10.55 | 3.40 | 5.17 | 3.16 | 8.01 | 4.09 | 1.53 |
注)分析期間や為替、ハンセン中企、台湾、韓国の定義は表1と同じ。乖(t-1)~乖(t-2)は乖離率(t-1)、乖離率(t-2)。それぞれ1日前、2日前の乖離率。決定係数は自由度調整済。
出所)NRI SuperFocus、NRI Fundmark、Bloombergよりウエルス・スクエア作成。
不可日と乖離率のラグを変数として加えることで、説明力(決定係数)は向上し、各変数のt値も2を超えた。また、切片の回帰係数はゼロに近くなり、そのt値も有意ではなくなった。回帰係数の大きさは為替が少し低下した。不可日要因の係数はプラスで、不可日周辺は基準価額に比べて、市場価格がプレミアムになりやすいことを示していいる。また、乖離率ラグ変数の回帰係数は、乖離率(t-2)は乖離率(t-1)の半分程度で、値も共に1より小さいことから、当日の乖離率を低下させる方向に働いている。
なお、この分析では説明変数が多いので、変数間の相関(多重共線性、変数間の相関が高い)があるかどうかを検証してみたが、問題はなかった1 。また、自己回帰の変数も用いているので、定常性の確認も行ったが問題はなかった2 。
前述した概念式①、②を見ればわかるように、乖離率は投信の基準価額を算出するにあたっての一定の定義の上に成り立っているため、国内市場を対象としたETFと海外市場を対象にしたETFとでは乖離率と意味が異なる。今回の分析からすると、当日中に翌日の新興国株投信の基準価額を一部反映していると言える。また、不可日や乖離率のラグ効果も認識しておいた方がよいだろう。
11月5日には、市場の取引時間が現在の15時から15時半に延長される。これによって、香港やインドとの重複時間が増えることから、より織り込み度合が強くなるだろう。
1変数間の多重共線性を確認するために、VIF(Variance Inflation Factor、分散拡大係数)を計算した。ある変数を残りの変数で重回帰分析を行い、VIF=1/(1-決定係数)で算出する。この値が1に近ければ多重共線性は問題はなく、5を超えると多重共線性が疑われる。決定係数がゼロに近いということは、ある変数が他の変数で説明されないということでもある。ちなみに、今回の分析でのVIF値は1.04~1.90の間であった。
2表2では、乖離率をt-2まで使っているが、乖離率t-3までを考慮して、定常性の確認を行ったところ、乖離率t-2までが有効であった。
(2024年10月25日作成)


