負けないためのETF投資戦略
外債投資と為替【ETF投資戦略⑥】
この記事は、約5分で読めます
為替変動が小さくなって久しい。それゆえ、外債投資では、為替ヘッジをしない方が、為替ヘッジをした場合に比べ、リスク量が小さくなる現象もみられるようになってきた。この現象が持続すれば、運用戦略やリスク管理にも影響を与えるだけに、今回はこの現象について分析を行いたい。
図1に、外債(為替ヘッジ無、円ベース)、外債H(為替ヘッジ有)、為替(円/ドルと円/ユーロを均等で保有)のリスク量の推移を示した。
図1 各資産のリスク推移(1995年12月末~2020年8月末)
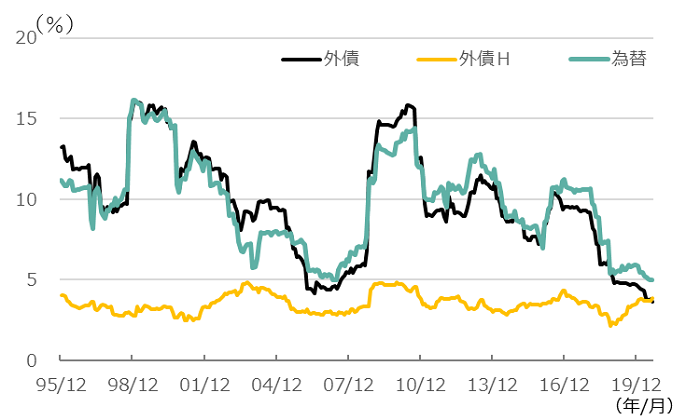
注)月次リターンの24か月ローリング。年率換算。ここで扱っている指数は、外債:FTSE世界国債インデックス(除く日本、ヘッジなし・円ベース)、外債H:FTSE世界国債インデックス(除く日本、円ヘッジ・円ベース)。
出所)Bloombergのデータより、ウエルス・スクエア作成
外債Hは2~5%の範囲で安定して推移している一方、外債の方は大きく変動している。直近は低下して、8月末では外債Hのリスク量をわずかに下回った。24か月ローリングという技術的要因もあろうが、過去には見られなかったことである。外債のリスク量の推移は、円/ドル、円/ユーロのリスク量の推移と同じような動きとなっており、為替のリスク量は近年低下傾向にある(ちなみに外債に占める通貨配分はドルとユーロで同じ程度の割合であり、合わせて80%以上を占めている)。
外債のリスク量は、現地通貨建て債券のリスク量、為替のリスク量、現地通貨建て債券と為替のリターンの相関関係(共分散)の総和である。そこで、図2で現地通貨建て債券の代替として外債Hを使って、為替との間のリターンの相関関係の推移を示した。
図2 外債Hと為替の相関係数の推移(1995年12月末~2020年8月末)
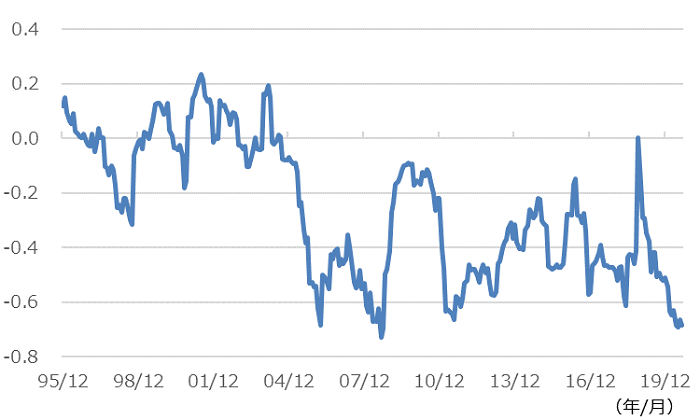
注)月次リターンの24か月ローリングで計測。縦軸は相関係数。相関係数は―1~+1の間で推移。0だと無相関。正だと同じ方向に動きやすく、負の値だと逆の方向に動きやすい。
出所)Bloombergのデータより、ウエルス・スクエア作成。
2000年代の半ば以降の相関は、-0.2 ~ -0.7を推移していることがわかる。先に述べたようにリスク量は、3つの要因で成り立っており、外債Hと為替の間のリターンの相関がマイナスだと、リスク量は小さくなる。直近は為替のリスク量が低下し、外債Hのリスク量に近づいたことで、為替ヘッジをしない外債のリスク量が外債Hより小さくなったわけである(興味のある方は巻末の(ご参考)を参照されたい)。
為替自体のリスク量の低下要因として、そのファンダメンタル要因である内外物価上昇率の格差が縮小してきていることが挙げられよう。図3に日米消費者物価(コア)上昇率及びその格差の推移を示した。
図3 日米消費者物価(コア)上昇率及びその格差推移(1971年1月末~2020年7月末)
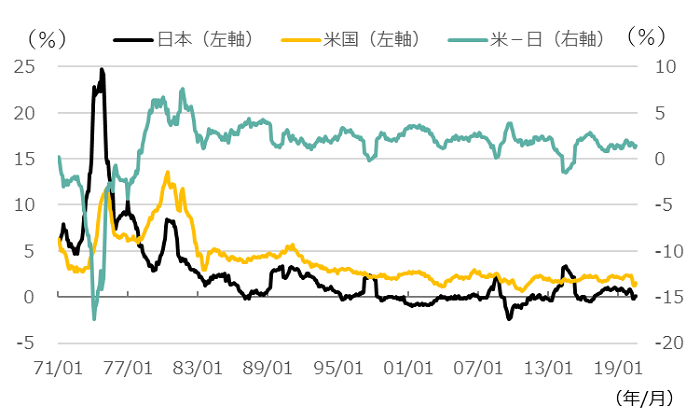
注)前年同月比。
出所)野村総合研究所SuperFocusのデータより、ウエルス・スクエア作成。
70年代は日米ともに消費者物価上昇率の水準が高く、特に第一次石油危機の時は日本の方が高かった。その後、第二次石油危機を日本がいち早く脱した。その後は徐々に日米共に上昇率は低下しているものの、米国の方が高い状況が続いている。一方、日本もデフレ対策を取ったことで、その上昇率格差は縮小している。そうしたことも、為替リスクの低下に寄与しているものと見られる。
以上を踏まえると、従来以上に外債を為替ヘッジする・しないについては、ヘッジコストの低下も踏まえ、より柔軟な対応が求められよう。運用戦略のみならず、リスク管理でも留意したいものである。
(ご参考)
1通貨で考えてみよう。現地通貨ベースの債券のリスクをσL、円からみた当該通貨の為替リスクをσE、債券と為替のリターンの相関係数をρとする。そして、為替リスクσE=kσL(為替リスクが債券リスクのk倍)と表せば、為替ヘッジをしない外債のリスクをσPとすると、その分散(リスクの2乗)は、
σP2=σL2+σE2+2ρσLσE
=σL2+k2σL2+2ρkσL2
=σL2(1+k2+2ρk) ①
と表すことが出来る。外債Hのリスクを現地通貨の債券のリスクで近似できるとすれば、外債のリスクが外債Hのリスクより小さくなるのは以下の不等式が成り立つ場合である。
σp2<σL2 ②
①を②の左辺に代入し、両辺をσL2で除すると、
1+k2+2ρK<1
となり、これを変形すると、k>0より、
ρ<-k/2 ③
となるとき、外債のリスクは外債Hのリスクより小さくなる。
例えば、現地通貨ベースの債券のリスクと為替リスクが同程度とすれば、k=1であり、③に代入すると、ρ<-1/2 ④となる。
この債券と為替のリターンの相関係数が-0.5より小さい環境下では、外債のリスクが外債Hのリスクより小さくなる。直近は、図1で見るように、④の条件を満たすような状態である。一方、以前のように為替リスクが債券リスクの2倍より大きい場合、相関係数ρが下限の-1でも、③の不等式は必ず成立せず、外債のリスクは外債Hのリスクより大きくなる。
(2020年9月作成)

